這回寫到的霍夫曼編碼是在Algorithms Illuminated Part 3: Greedy Algorithms and Dynamic Programming中讀到，乍看之下不會聯想到貪婪演算法，但它也是使用貪婪策略。在寫演算法前，先前情提要一些資料編碼的內容。

無失真資料壓縮

不論是在傳輸、下載或儲存檔案，我們都希望能做到無失真資料壓縮(lossless compression)，也就是在不影響內容的情況下壓縮資料，壓縮得多，自然時間、空間的效率也高。

資料在電腦中會被編碼為位元(0與1)組成的字串，而霍夫曼編碼提供一種較有效率的編碼方式，也就是以較少的位元進行編碼，進而可以實現無失真資料壓縮。

固定長度碼與可變長度碼

如果要為資料中的每個符號編碼，最直覺的方式可能是給每個符號固定長度的編碼(fixed-length coding)，例如長度固定為四的二元碼中，a, b, c, d 可能是 0000, 0001, 0010, 0011。

如果想要增進編碼效率，可以嘗試不要固定長度，而使用較少位元。例如同樣的a, b, c, d 可以是0, 01, 10, 1。這樣的可變長度碼(variable-length code)雖然更精簡，但它的問題在於無法確切知道每個碼如何切分，所以解讀上可能會有些問題。例如看到0的時候，有可能代表a，也有可能跟後面的1組成b。

因此，除了長度縮短外，我們還希望編碼是無前綴碼(prefix-free code)[註1]，也就是任兩個編碼不會是彼此的前綴(例如上述的0就是01的前綴)，這樣在解讀上就不會有模糊地帶。

比起固定長度碼，可變長度、無前綴碼在符號的出現頻率有差異時效率較高。例如以英文字母來說，a, e出現頻率可能遠高於y, z，有這樣的差異時，可變長度、無前綴碼可以增進編碼效率。而霍夫曼編碼即是可找到這種最佳無前綴碼的一種方式。

二元樹

我們可以用二元樹來表示上面提到的編碼，以下圖[註2]來說，樹中的每個節點連到左邊子節點的邊為0，連到右邊子節點的邊為1。我們可以利用邊來表達一符號的編碼，例如根節點到符號A經過兩個0的邊，代表A的編碼為00。

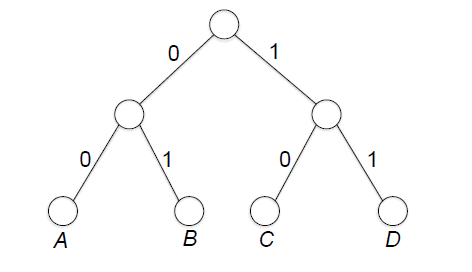
樹中沒有子節點的節點被稱為葉節點，而我們可以從「符號都只在葉節點上」來得知這些編碼為無前綴碼，因為如果有的編碼是其他編碼的前綴(例如a為0，b為01)，則為前綴的符號就不會在葉節點上(a會是b的父節點)。

霍夫曼樹

霍夫曼樹也是同樣的二元樹結構。從節點開始，逐步合併樹，直到合併出一棵霍夫曼樹來代表最佳編碼。它的步驟是：

1. 以n個樹代表要編碼的n個符號，該符號出現的頻率則為權重。
2. 以一個新節點將n個樹中權重最小的兩個樹合併，新節點的權重為兩個樹的權重和。
3. 重複步驟2，直到只剩下一棵樹。樹中所有節點左邊的邊為0，右邊的邊為1。

以下圖為例，以五個樹代表五個符號，旁邊的數字為出現頻率，也就是代表該符號的權重。接著將權重最小的D和E合併、權重加總，此時樹的總數變成4，接著合併權重最小的B和C。以此類推，不斷合併直到最後的霍夫曼樹，再為邊標上0和1，就可以得到平均長度最短的無前綴碼，舉例來說，C的編碼即為101。

圖片來源：維基百科

從霍夫曼樹的圖中可以看出幾個特點：

• 所有的樹被當作葉節點開始，由下而上合併，確保編碼為無前綴碼。

• 由權重最小的樹開始合併，因此頻率低的符號編碼較長，頻率高的符號編碼較短。

那講了那麼多，霍夫曼編碼「貪婪」的部分到底在哪裡呢？

在於每一步都盡可能讓樹的高度最少地增加。樹的高度越高，整體編碼會越長，可以想像當樹都只在同一邊合併的話，就會變得很高，雖然也可以得到無前綴碼，但不是最有效率解。霍夫曼編碼透過每一次合併權重和最小的樹，讓平均樹高的增加減到最小，也確保運算出平均長度最短的無前綴碼。

[註1]無前綴碼(prefix-free code)也稱作前綴碼(prefix code)，但為了避免誤會兩者為相反的意思，本文中選擇用無前綴碼一詞表達。
[註2]Tim Roughgarden, Algorithms Illuminated Part 3: Greedy Algorithms and Dynamic Programming, Soundlikeyourself Publishing, 2019, page 28.